Once a candidate has completed an application, five Evaluation Panel members will be assigned to score each application that is determined valid or eligible during our Administrative Review process. Evaluation Panel members will offer both scores and comments for each of four distinct traits in our rubric. Each of the four traits will be scored on a 0-5 point scale, in increments of 0.1. Those scores will combine to produce a total score. Examples of possible scores for a trait are… 0.4, 3.7, 5.0, etc.

The most straightforward way to ensure that every candidate is treated by the same set of standards would be to have the same Evaluation Panel members score every valid application; unfortunately, due to the number of candidates that we will receive, that is not possible.

Since the same candidates will not be scored by every Evaluation Panel member, the question of fairness needs to be carefully explained. One Evaluation Panel member scoring a candidate may have a more critical disposition, giving every assigned candidate a range of scores only between 1.0 and 2.0, as an example; meanwhile, another Evaluation Panel member may be more generous and score every candidate between 4.0 and 5.0. 

For illustrative purposes, let’s look at the scores from two hypothetical judges:

 

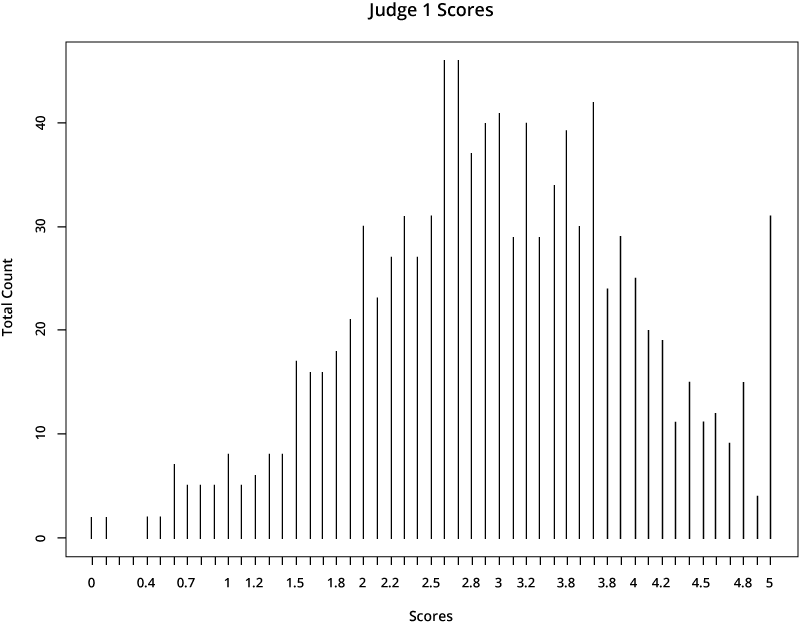
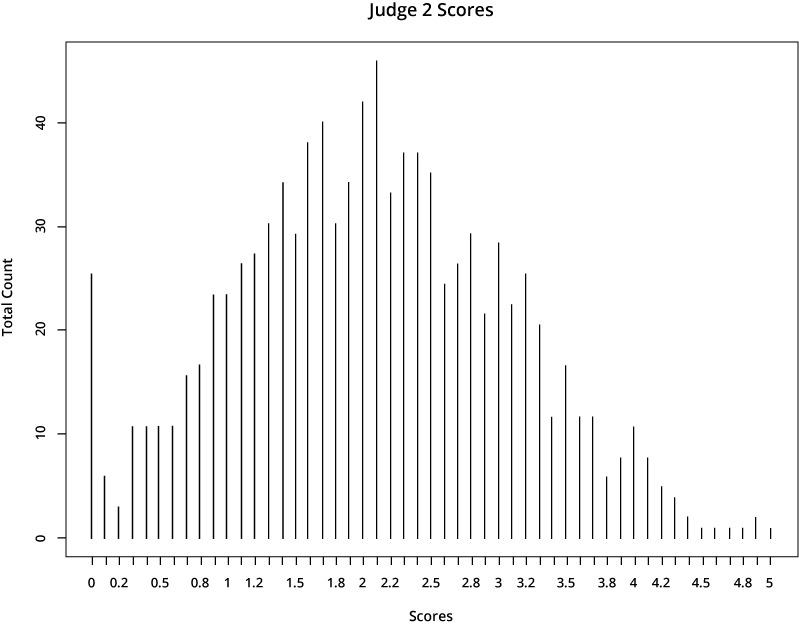
The first judge is far more generous in scoring than the second one, who gives much lower scores. If a candidate’s application was rated by the first judge, it would earn a much higher total score than if it was assigned to the second judge.

We have a way to address this issue. We ensure that no matter which judges are assigned, each valid application will be treated fairly. To do this, we utilize a mathematical technique relying on two measures of distribution, the mean and the standard deviation.

The mean takes all the scores assigned by a judge, adds them up, and divides them by the number of scores assigned, giving an average score.

Formally, we denote the mean like this: 

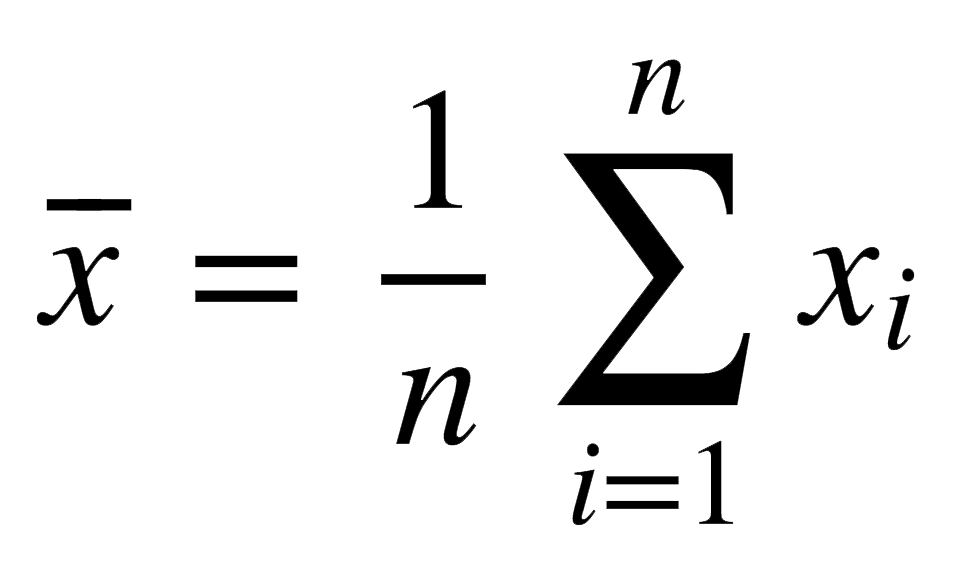
The standard deviation measures the “spread” of a judge’s scores. As an example, imagine that two judges both give the same mean (average) score, but one gives many zeros and fives, while the other gives more ones and fours. It wouldn't be fair, if we didn’t consider this difference.

Formally, we denote the standard deviation like this: 

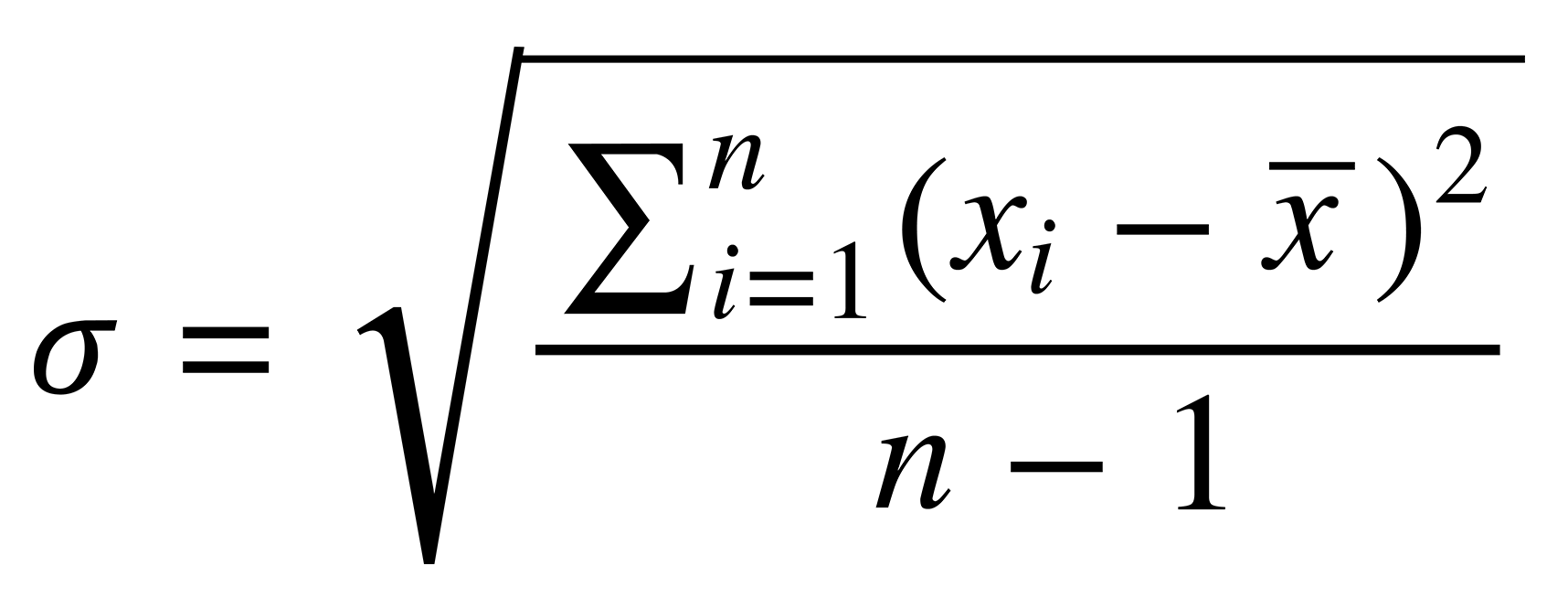
To ensure that the judging process is fair, we rescale all the scores to match the judging population. In order to do this, we measure the mean and the standard deviation of all scores across all judges. Then, we change the mean score and the standard deviation of each judge to match.

We rescale the standard deviation like this:

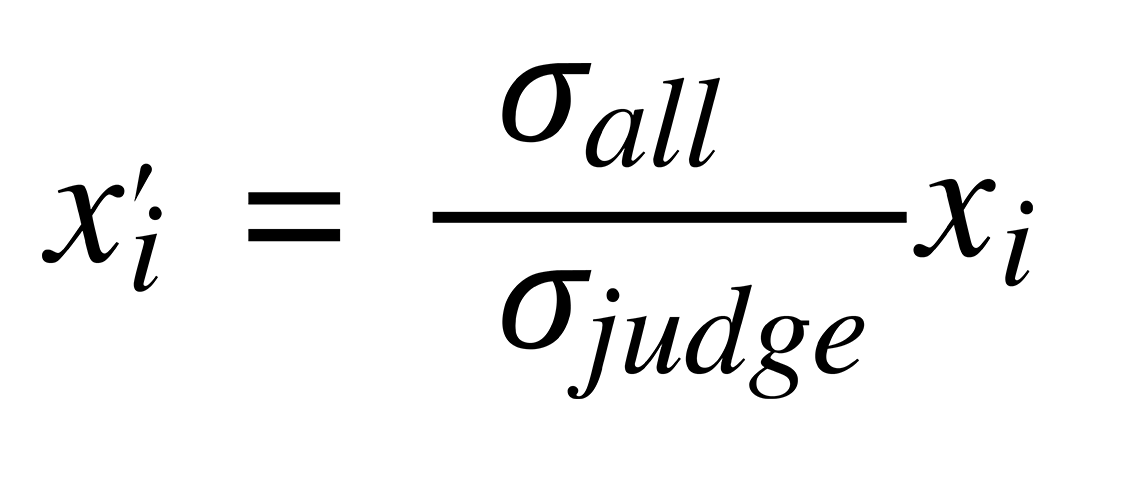
Then, we rescale mean like this:

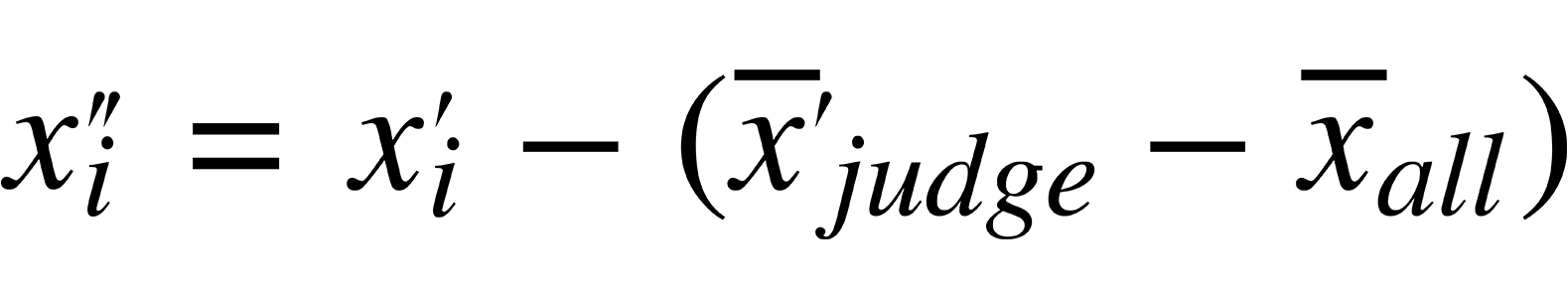
Basically, we are finding the difference between both distributions for a single judge and those for all of the judges combined, then adjusting each score so that no one is treated unfairly according to which judges they are assigned.

If we apply this rescaling process to the same two judges in the example above, we can see the outcome of the final resolved scores. They appear more similar, because they are now aligned with typical distributions across the total judging population.

 

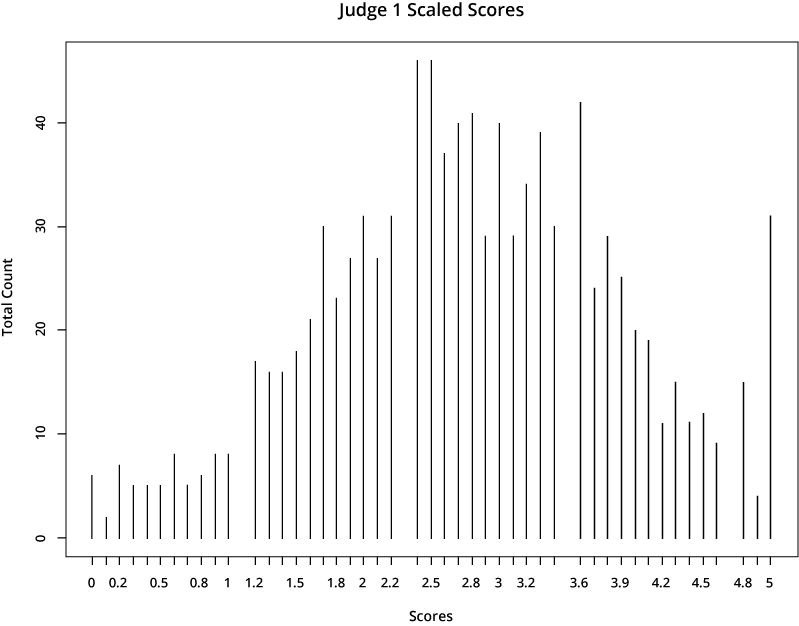
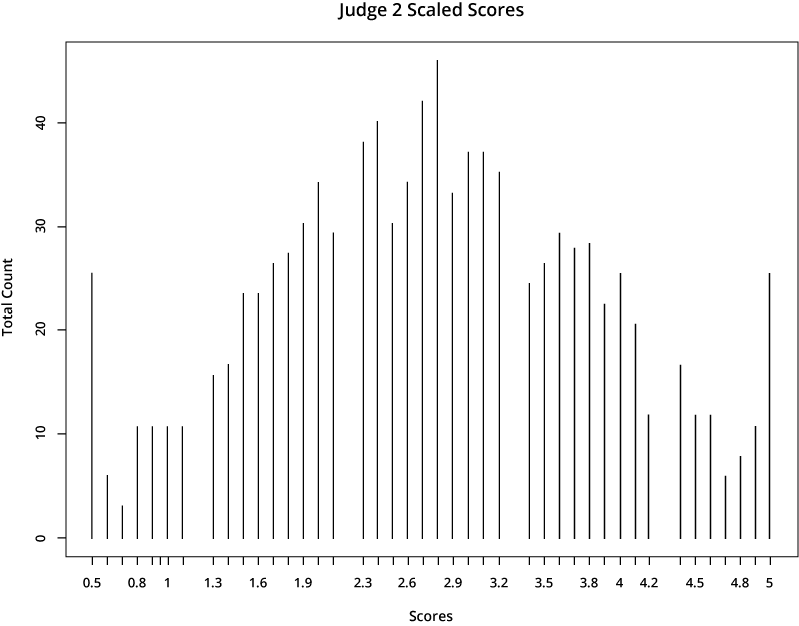
We are pleased to answer any questions you have about the scoring process. Please feel free to ask any questions on the discussion board. Please REGISTER today to begin developing your application.